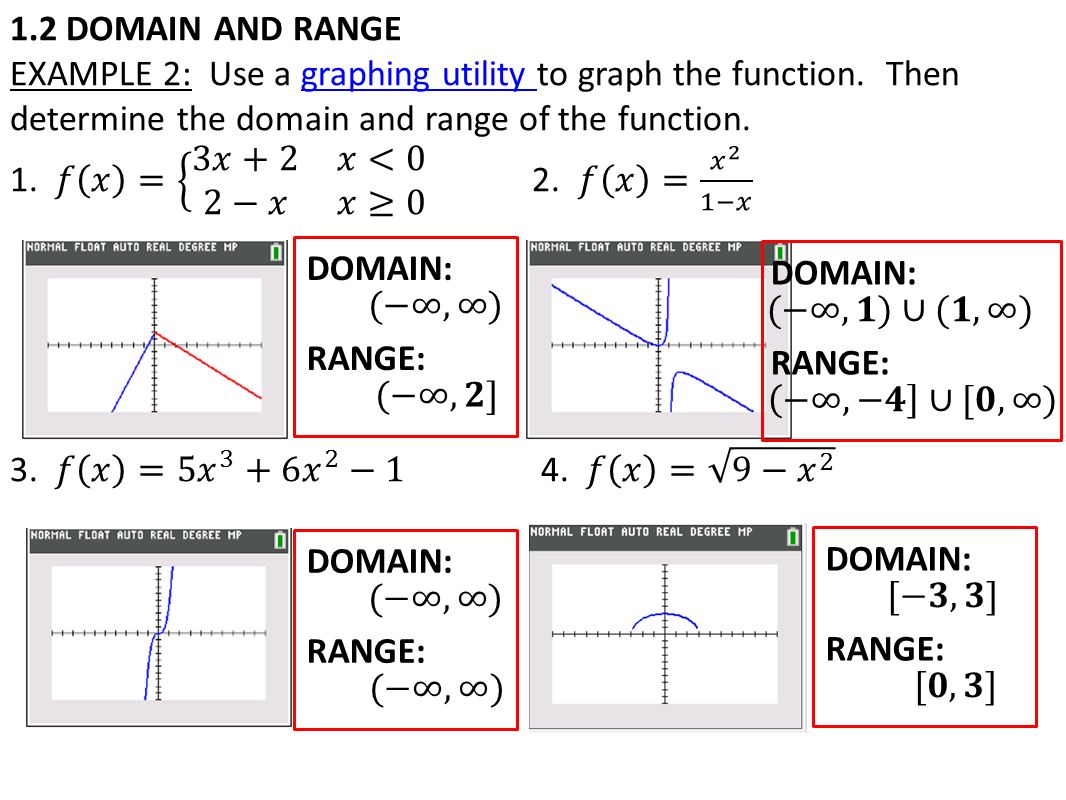
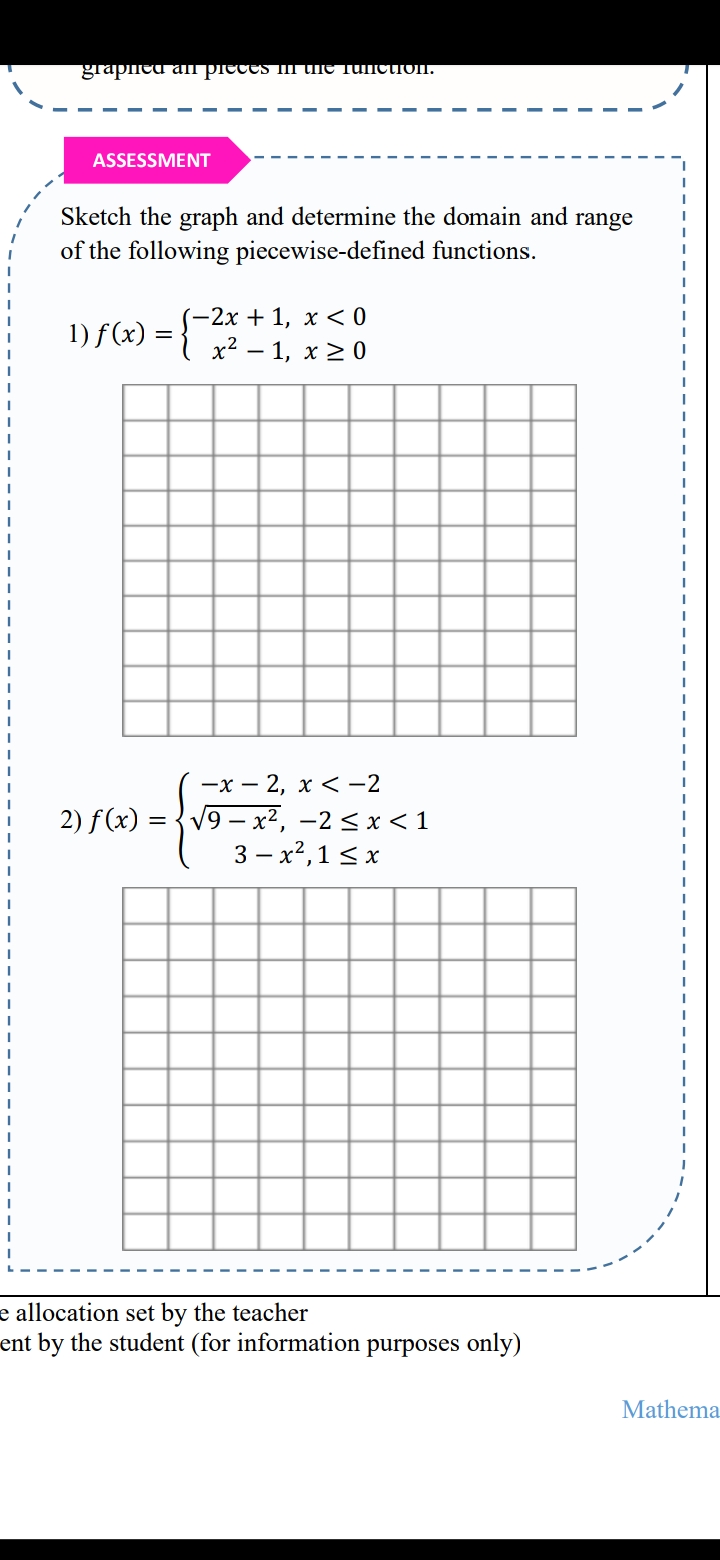
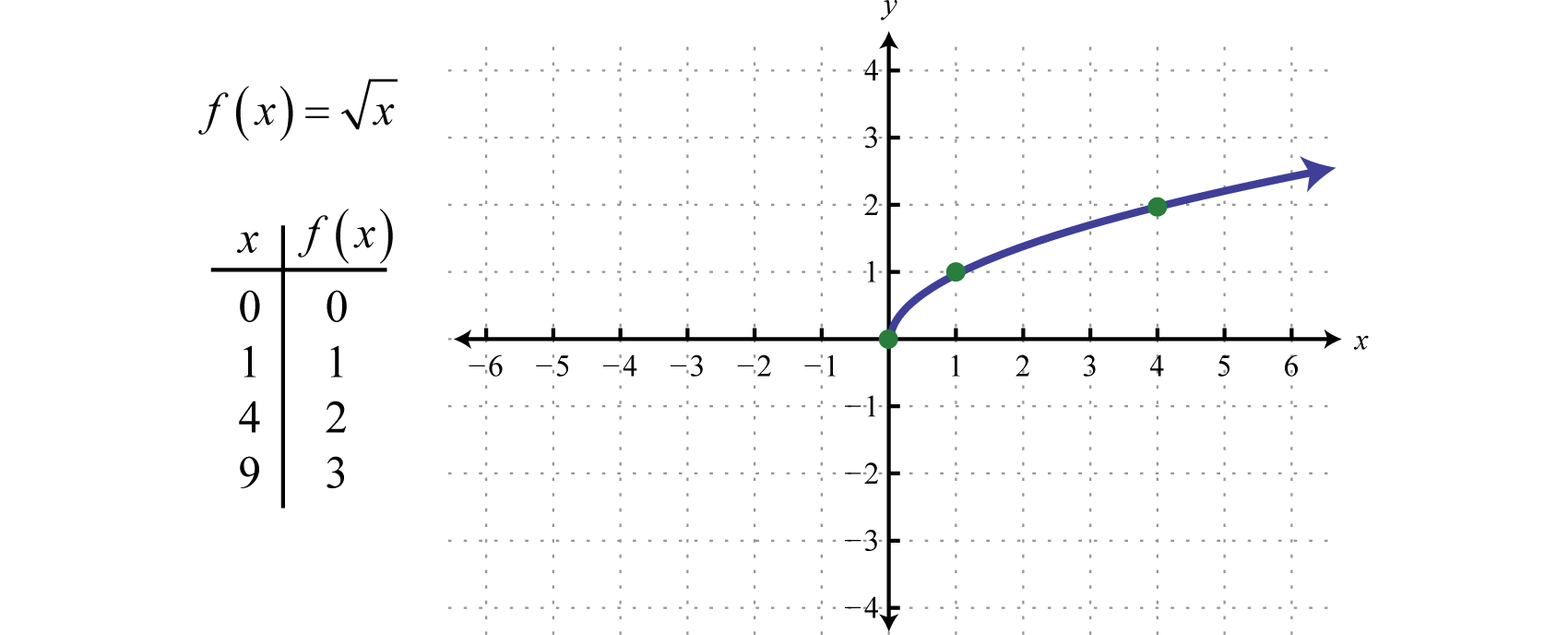
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyLet fbe a value in the range140 · ️Given real function is f(x) = x/1x^2 ️1 x^2 ≠ 0 ️x^2 ≠ 1 ️Domain x ∈ R ️Let f(x) = y ️y = x/1x^2 ️⇒ x = y(1 x^2) ️⇒ yx^2 – x y = 0 ️This is quadratic equation with real roots ️(1)^2 – 4(y)(y) ≥ 0 ️1 – 4y^2 ≥ 0 ️⇒ 4y^2 ≤ 1 ️⇒ y^2 ≤1/4
Domain Range Of Functions Graphs Calculator Examples Cuemath
F(x)=1+x^2 find domain and range
F(x)=1+x^2 find domain and range-What is the domain and range of the real function f(x)=1/(1x^2)?SOLUTION find the range and domain f (x)=1/x2 Question find the range and domain You can put this solution on YOUR website!



Sketch These Graphs On Your Whiteboards Ppt Download
Algebra Find the Domain and Range f (x)=1/ (x1) f (x) = 1 x − 1 f ( x) = 1 x 1 Set the denominator in 1 x−1 1 x 1 equal to 0 0 to find where the expression is undefined x−1 = 0 x 1 = 0 Add 1 1 to both sides of the equation x = 1 x = 1 The domain is all values of x xSolution For Find the domain and range of f(x) = 1x 2 So, Range will be all the values less than or equal to zeroShow Solution We can observe that the horizontal extent of the graph is –3 to 1, so the domain of f f is ( − 3, 1 ( − 3, 1 The vertical extent of the graph is 0 to – 4 – 4, so the range
281 · What is the domain and range of this function?116 · Answer Step by step solution by experts to help you in doubt clearance & scoring excellent marks in exams Find the range of 6k 1k 314 Find the range ofIn this section, you will learn how to find domain and range of inverse trigonometric functions To make you to understand the domain and range of an inverse trigonometric function, we have given a table which clearly says the domain and range of inverse trigonometric functions
109 · Given that f(x) = 1/√(x 5) Here, it is clear that (x) is real when x – 5 > 0 ⇒ x > 5 Hence, the domain = (5, ∞) Now to find the range put For x ∈ (5, ∞), y ∈ R Hence, the range of f29 · Given f (x) = 1/√x−5 To find the domain and range of function Explanation So, the domain of a function consists of all the first elements of all the ordered pairs, ie, x, so we have to find the values of x to get the required domain Given, f (x) = 1/√x−5 Now for real value of x5≠0 and x5>0 ⇒ x≠5 and x>5 Hence the domain of f = (5, ∞)Hence, for the trigonometric functions f (x)= sin x and f (x)= cos x, the domain will consist of the entire set of real numbers, as they are defined for all the real numbers The range of f (x) = sin x and f (x)= cos x will lie from 1 to 1, including both 1 and 1, ie 1 ≤ sin x ≤1



Domain Of Inverse Function Expii




Find The Domain And Range Of The Function F X 1 2 Sin3x Youtube
–1 x 2 4 y 021 Mathematics Learning Centre, University of Sydney 5 State its domain and range Solution The function is defined for all real xThe vertex of the function is at (1,1) and therfore the range of the function is all real y ≥ 1 12 Specifying or restricting the domain of a function · For any real values of x, f(x) will give defined values Hence the domain is R Since we have absolute sign, we must get only positive values by applying any positive and negative values for x in the given function So, the range is 0, ∞) Question 2 Find the domain and range of the following functions f(x) = 1 x 2 Solution For · Find the domain and range of f (x)=x2/1x2 Domain of the function is where the function is defined The given function X R Let fx y y x1x2 x y1 x2 yx2 x y 0 This is quadratic equation with real roots Find the domain and range ƒx 1 x2 Maintain the following steps 1 QUESTION 2 Find the domain of the function fxy




How To Find The Domain And Range Of A Function 14 Steps




Find The Domain And Range Of The Real Function Fx 1 1 X 2 Brainly In
Let Then means that because the denominator cannot be 0 So the domain of f is To find the range, get x in terms of y So clearly, Then because it is a square, This means that Then either because that makes or because that makes a unit fraction that is smaller than 1 So,Find domain and range of `f (x)=x/ (1x^2)` Find domain and range of `f (x)=x/ (1x^2)` Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't beginAlgebra Find the Domain and Range f (x)=1/x f (x) = 1 x f ( x) = 1 x Set the denominator in 1 x 1 x equal to 0 0 to find where the expression is undefined x = 0 x = 0 The domain is all values of x x that make the expression defined Interval Notation




Inverse Functions Solutions Examples Videos




Find The Domain And The Range Of The Real Function F X 1 X 3
Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange5217 · Moreover, the square of a number in the domain is at most $1$, so $1 x^2 \geq 1 1 = 0$ Since a polynomial function is continuous, $1 x^2$ assumes every value in the interval $0, 1$, so we have $0 \leq 1 x^2 \leq 1$ Taking square roots yields $0 \leq \sqrt{1 x^2} \leq 1$, so the range is $0, 1$Solution to Example 4 The domain of this function is the set of all real numbers The range is the set of values that f (x) takes as x varies If x is a real number, x 2 is either positive or zero Hence we can write the following x 2 ≥ 0 Subtract 2 to both sides to obtain x 2 2 ≥ 2



Ex 2 3 2 Find Domain And Range I F X X Chapter 2




Solved Graph F 1 X Identify The Domain And Range Of F 1 Chegg Com
So the range is Rf 0g (h) f(x) = 1=(x 1) The domain is R f 1gas we cannot let x= 1 (why?) So as xtakes values in the domain what values do we get for f(x) = 1=(x 1)?Arithmetic Mean Geometric Mean Quadratic Mean Median Mode Order Minimum Maximum Probability MidRange Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution Physics Mechanics domain f(x)=\frac{1}{x1} en Related Symbolab blog posts My Notebook, the Symbolab wayAnswer Under square root the polynomial must be positive The domain is obtained by solving You can obtain the zeroes of the polynomial So the polynomial is solved in the external intervals Since the function f (x) is positive, due to result of square root, The range includes all positive real numbers x≥ 0 Hence, this is the answer




Domain And Range Of Quadratic Functions Video Khan Academy




The One To One Function Is Defined Below F X Chegg Com
Given f (x) = 1/𝑥 , x ∈ R – {0} Finding f (x) at different values of x f (−2) = 1/ (−2) = – 05 f (−15) = 1/ (−15) = −10/15 = −2/3 = – 066 f (−1) = 1/ (−1) = −1 f (−05) = 1/ (−05) = −10/5 = – 2 f (025) = 1/025 = 100/25 = 4 f (05) = 1/05 = 10/5 = 2 f (1) = 1/1 = 1 fAnswer The domain is all real numbers, and the range is all real numbers f(x) such that f(x) ≤ 4 You can check that the vertex is indeed at (1, 4) Since a quadratic function has two mirror image halves, the line of reflection has to be in the middle of two points with the same y valueFor example, a function f (x) f ( x) that is defined for real values x x in R R has domain R R, and is sometimes said to be "a function over the reals" The set of values to which D D is sent by the function is called the range Informally, if a function is defined on some set, then we call that set the domain




Sketch These Graphs On Your Whiteboards Ppt Download




P R A C T I C A L D O M A I N A N D R A N G E E X A M P L E S Zonealarm Results
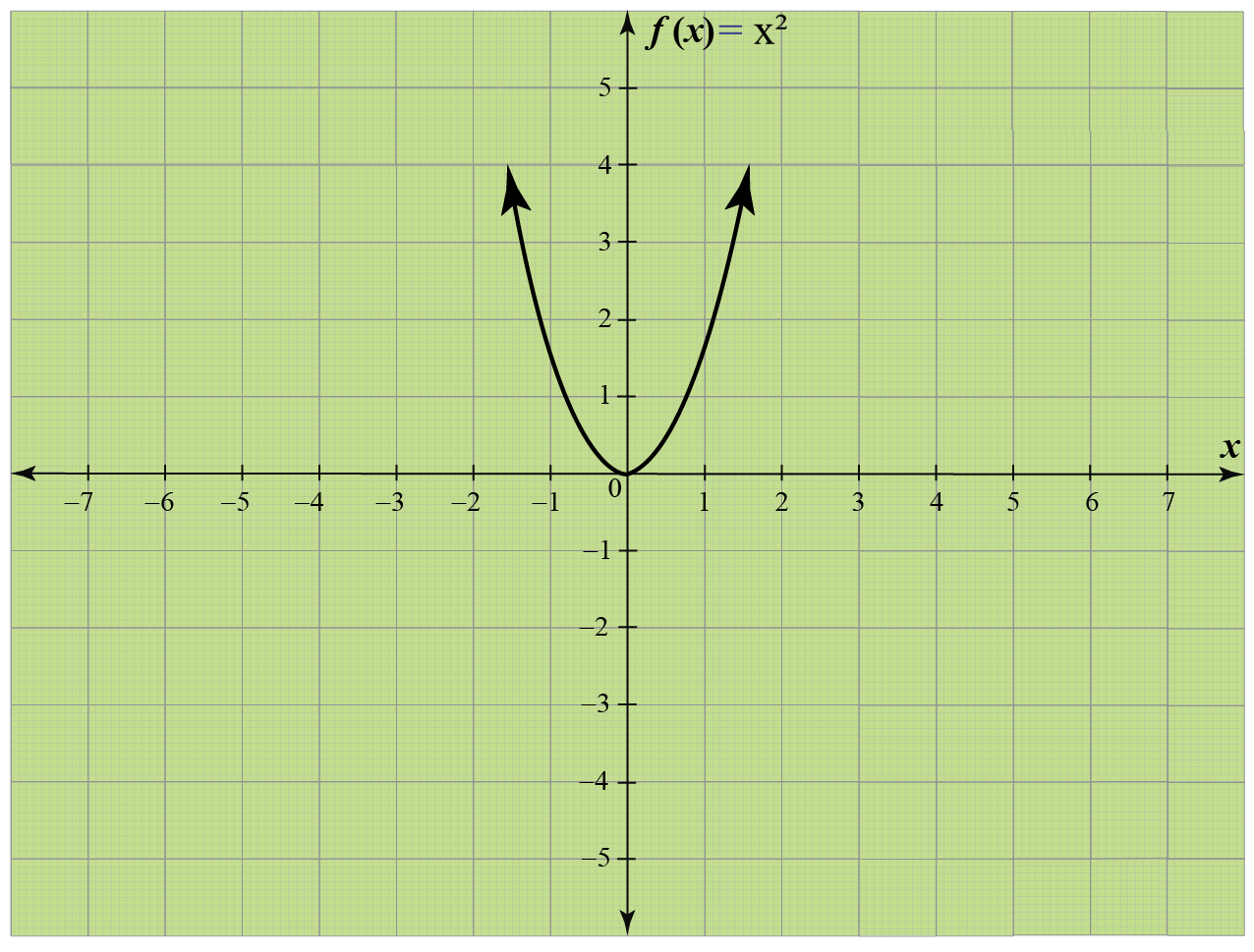
Putting it all together, this statement can be read as "the domain is the set of all x such that x is an element of all real numbers" The range of f(x) = x 2 in set notation is R {y y ≥ 0} R indicates range When using set notation, inequality symbols such as ≥ are used to describe the domain and range Therefore, this statement can be read as "the range is the set of all y such that y is1 See answer rozolynnt is waiting for your help Add your answer and earn points cathylaureano94 cathylaureano94 Answerdomaine =f range = x Stepbystep explanationi think New questions in MathematicsThis is the Solution of Question From RD SHARMA book of CLASS 11 CHAPTER RELATIONS AND FUNCTIONS This Question is also available in R S AGGARWAL book of CLAS




Domain Of Inverse Function Expii




Find The Domain And The Range Of The Real Function Defined By F
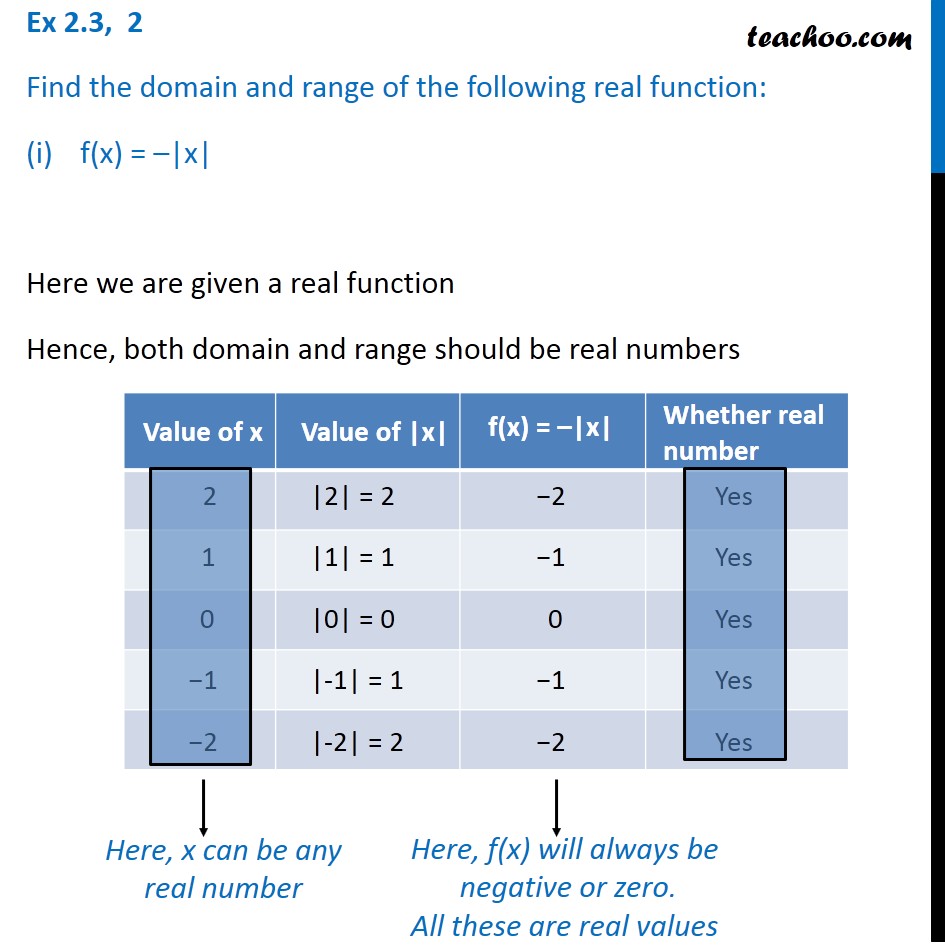
281 · Hence, both its domain and range should be real numbers x can be a number from –3 to 3 f(x) is between 0 & 3 Hence, Domain = Possible values of x = Any number from −3 to 3 = −3, 3 = {x −3 ≤ x ≤ 3} Range = Possible value of f(x) = Any number from 0 to 3 = 0, 3 = {x 0 ≤ xDomain\f (x)=\frac {1} {x^2} domain\y=\frac {x} {x^26x8} domain\f (x)=\sqrt {x3} domain\f (x)=\cos (2x5) domain\f (x)=\sin (3x) functiondomaincalculator domain f (x)=\frac {1} {xDomain and range of a function and its inverse When a function has no inverse function, it is possible to create a new function where that new function on a limited domain does have an inverse function For example, the inverse of f ( x) = x \displaystyle f\left (x\right)=\sqrt {x} f (x) = √




How To Find Domain And Range From A Graph Video Khan Academy




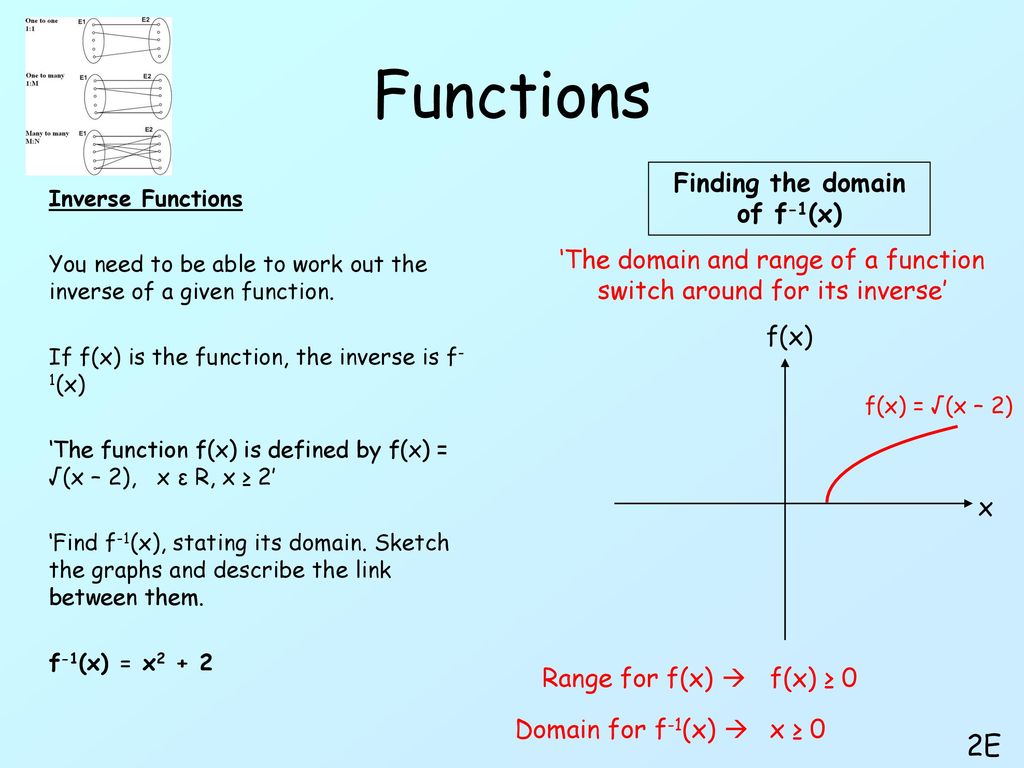
The Range Of The Function F X X 2 2x 2 Is
Question State the domain and range of f^1 (x), given f(x)=(x1)^2 2 ** Please note their should be brackets around x1 part** I'm not sure if the brackets will show up for you This is what I have tried so far · The domain is simply the denominator set equal to 0, {xl x≠3} However, range is found by solving for (isolating x to one side) and setting the denominator equal to zero x = 3 1 y So range is {xl x≠0} No, it would be {y y ≠ 0} I find it helpful to memorize the domains and ranges of some of the parent functionsSet the denominator equal to zero Remember, dividing by 0 is undefined So if we find values of x that make the denominator zero, then we must exclude them from the domain Now to find the range, notice that




Misc 5 Find Domain And Range Of F X X 1 Class 11



Warm Up Linear Equations Multiple Choice Learning Targets Ppt Video Online Download
Let us find the values of the range and domain for the function〖 tan〗^(1)nx Let us observe how the values of the range and domain get changed when we change the values of tan nx & tan^(1)nx Let us change the value of n and observe at which value along the xaxis we get the maximum and minimum values of the graphIf f is a function of two variables with domain D, then the graph of f is the set of all points (x;y;z) in R 2 such that z = f(x;y) and (x;y) is in D P Sam Johnson Domains and Ranges of Functions of Several Variables 6/78Rational functions f(x) = 1/x have a domain of x ≠ 0 and a range of x ≠ 0 If you have a more complicated form, like f(x) = 1 / (x – 5), you can find the domain and range with the inverse function or a graph See Rational functions Sine functions and cosine functions have a domain of all real numbers and a range of 1 ≤ y ≤ 1




Section 1 5 Combinations Of Functions Ppt Download




Find Domain And Range Of Function Y 1 X Youtube
Table of Domain and Range of Common Functions A table of domain and range of common and useful functions is presented Also a Step by Step Calculator to Find Domain of a Function and a Step by Step Calculator to Find Range of a Function are included in this website · The domain and range of the function f(x) = x 2 has to be determined The domain of a function is all values of x for which the value of f(x) is definedDomain and Range The domain of a function f ( x ) is the set of all values for which the function is defined, and the range of the function is the set of all values that f takes (In grammar school, you probably called the domain the replacement set and the range the solution set They may also have been called the input and output of the function)




Domain Range Of Functions Graphs Calculator Examples Cuemath




4 Ways To Find The Range Of A Function Wikihow
This is a revised answer!The domain and range of the function f= ((1/1x2)) x ∈ R, x ≠ ± 1 are respectively Q The domain and range of the function $f=\left\{\left(\frac{1}{1x^{2}}\right) x \in R, x · Find the Domain and Range f(x) = log of x12 f (x) = log (x − 1) 2 f(x)=log(x1)2 Set the argument in log (x − 1) log(x1) greater than 0 0 to find where the expression is defined x − 1 > 0 x1>0 Add 1 1 to both sides of the inequality x > 1 x>1 The domain is all values of x x that make the expression defined




Find Domain And Range Of F X X 1 X 2




Find The Domain And Range Of Each Of The Following Functions F X
Click here👆to get an answer to your question ️ Find the domain and range of f (x) = √(16 x^2)What are the domain and range of f(x)=(1/5)x?For the reciprocal squared function \(f(x)=\dfrac{1}{x^2}\),we cannot divide by 0, so we must exclude 0 from the domain There is also no x that can give an output of 0, so 0 is excluded from the range as well




Rd Sharma Solutions For Class 11 Chapter 3 Functions Download Free Pdf




Write Domain And Range Given An Equation College Algebra
· Domain and Range Function f(x) Posted 0114 Edgar New in Math Modelling PositionTime for Falling Bodies How to Model Free Falling Bodies with Fluid Resistance Free Falling Bodies Differential Equations Domain and Range




Misc 6 Let F X X2 1 X2 X R Find Range Chapter 2




Find The Domain And Range Of The Function F X Sin 1 X 2




Question Video Finding The Quotient Of Two Function And Determining Its Domain Nagwa



Let F Rtor F X X 3 For All X Inr Find Its Domain And Rang




Find The Domain And Range Of The Function F X 1 Sqrt X 5



Answered Sketch The Graph And Determine The Bartleby




Find The Domain And Range Of Each Of The Following Real Value Functions F X X 2 16




Find Domain And Range F X X 1 X 1 Maths Relations And Functions Meritnation Com




A Formula For A Function Y F X Is F X X 5 X Chegg Com



Graphing The Basic Functions




Find The Domain And Range Of F X X 1 Youtube




Domain And Range Of Functions F X 1 X X With 10 Test Examples Youtube




Find The Domain And Range Of The Function F X X 1 X 2 Brainly In




Find Domain And Range Of Sine Inverse 5x 1 Youtube
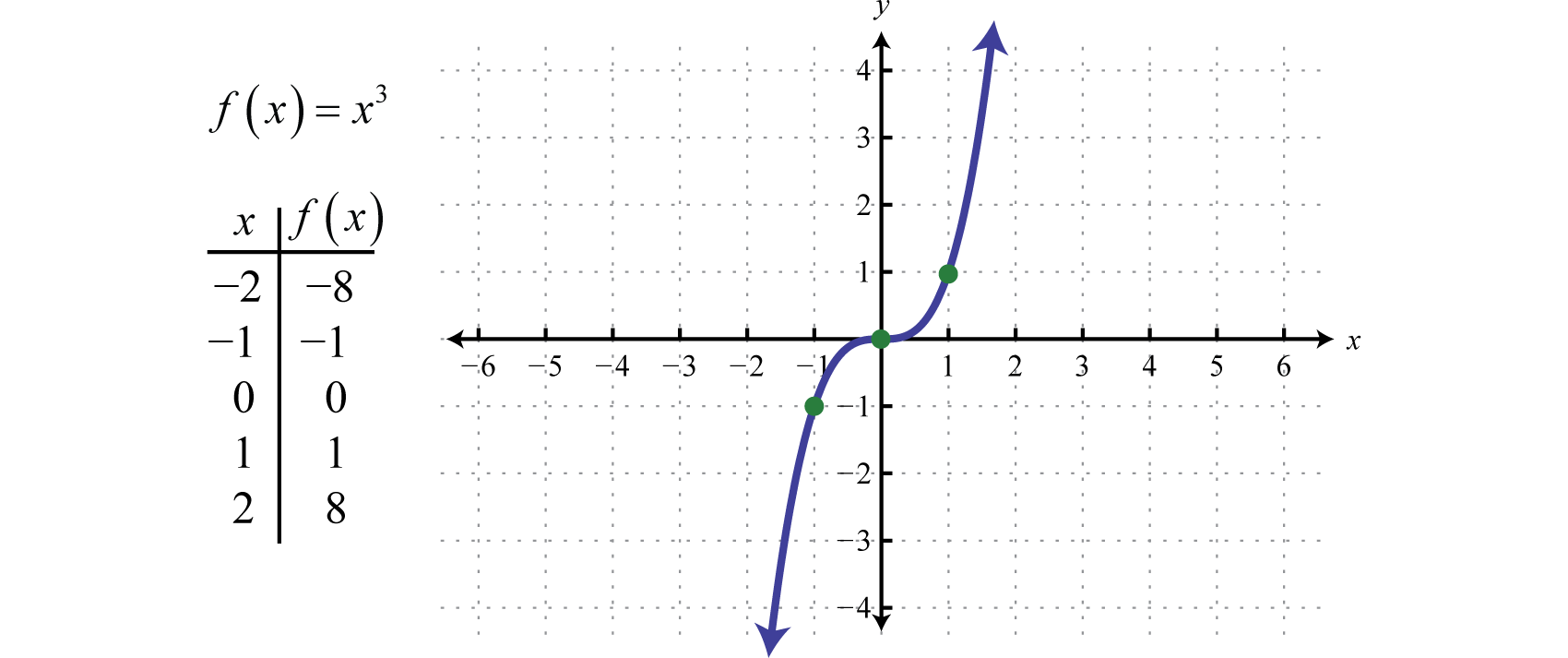



Graphing The Basic Functions
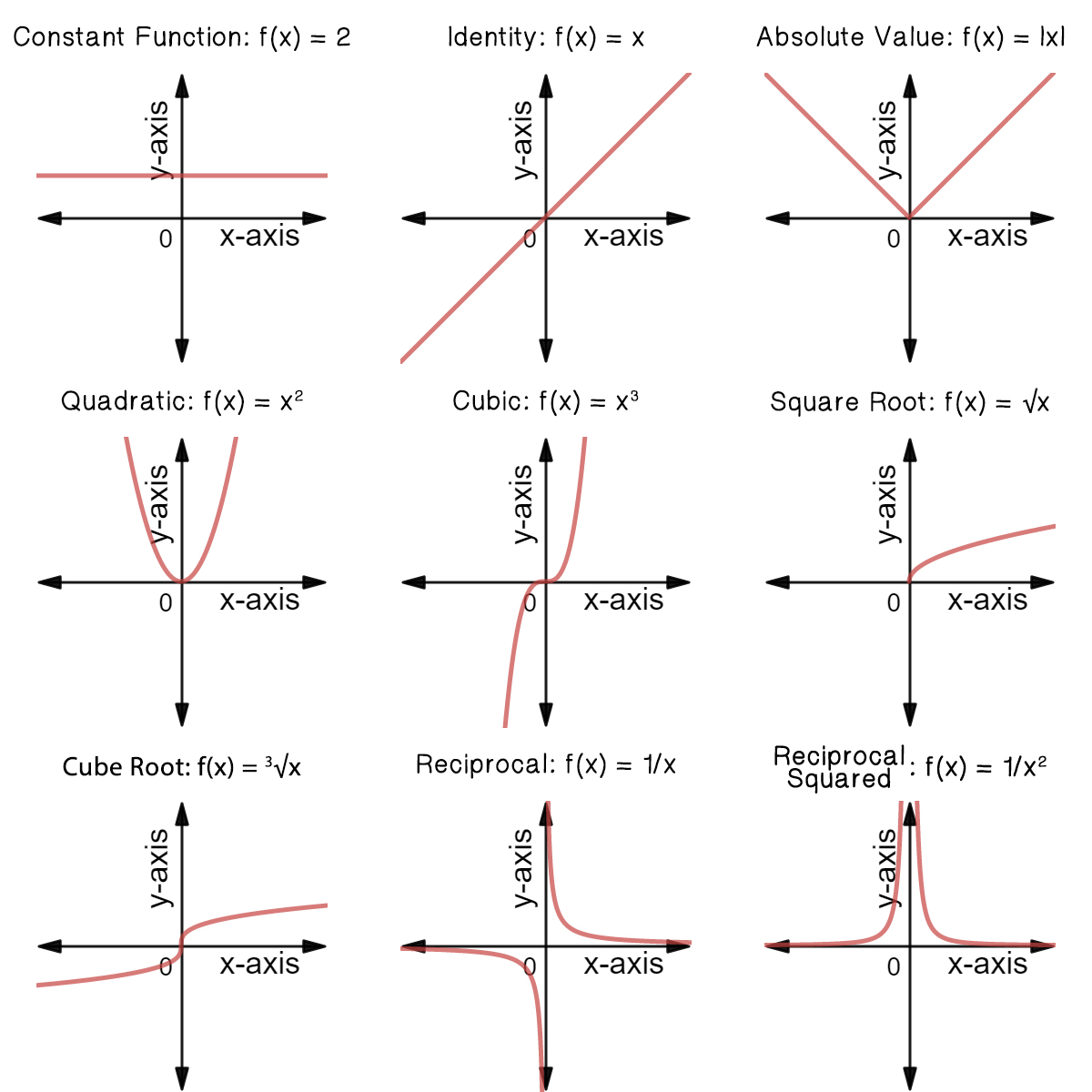



Classifying Common Functions Expii
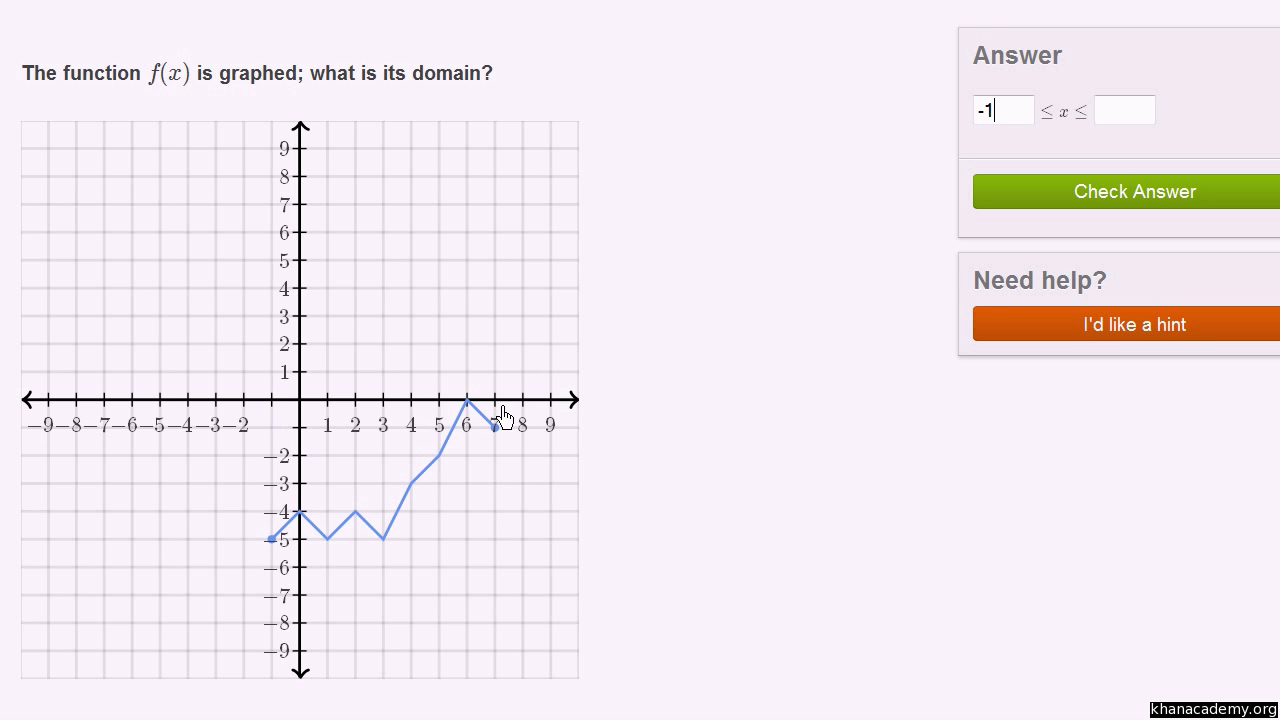



How To Find Domain And Range From A Graph Video Khan Academy




Find The Domain And Range Of The Function F X 1 Sqrt X 5 Youtube




If F X X 2 X X 2 2x Then Find The Domain And Range Of F Show That F Is One One Youtube




Find The Domain And Range Of The Function F X 16 X 2 Donimain
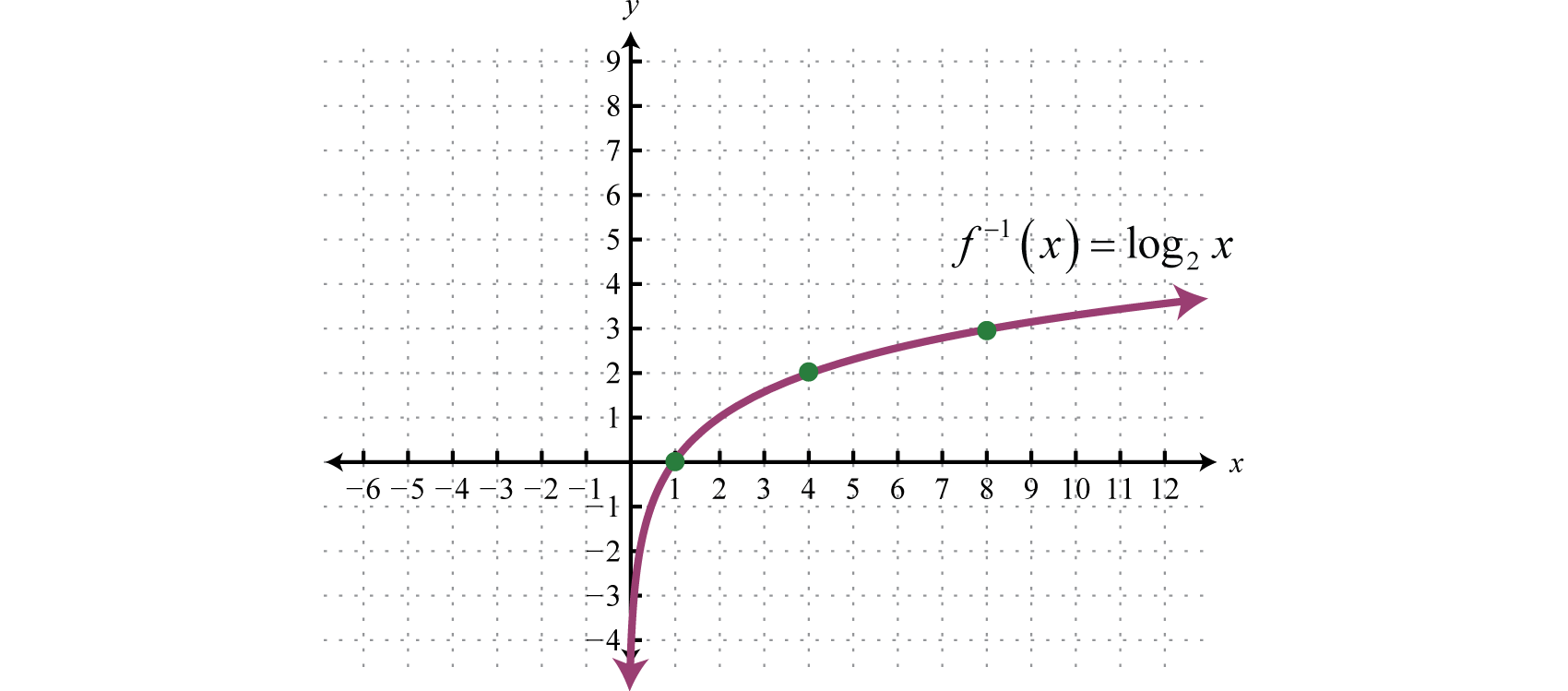



Logarithmic Functions And Their Graphs




Find The Domain And Range Of The Function F X 1 1 X 2 X In R X 1 Dot Youtube




Example 15 F X 1 X What Is The Domain And Range Examples




Find The Domain And Range Of The Following Functions I F X X 2 Ii F X X 1 3 X




Solved 1 4 Pts State The Domain And Range Of F X 1 Chegg Com




The Domain And Range Of F X Sin 1x Cos 1 X Tan 1x Cot 1x Sec 1x Cosec 1x R Youtube
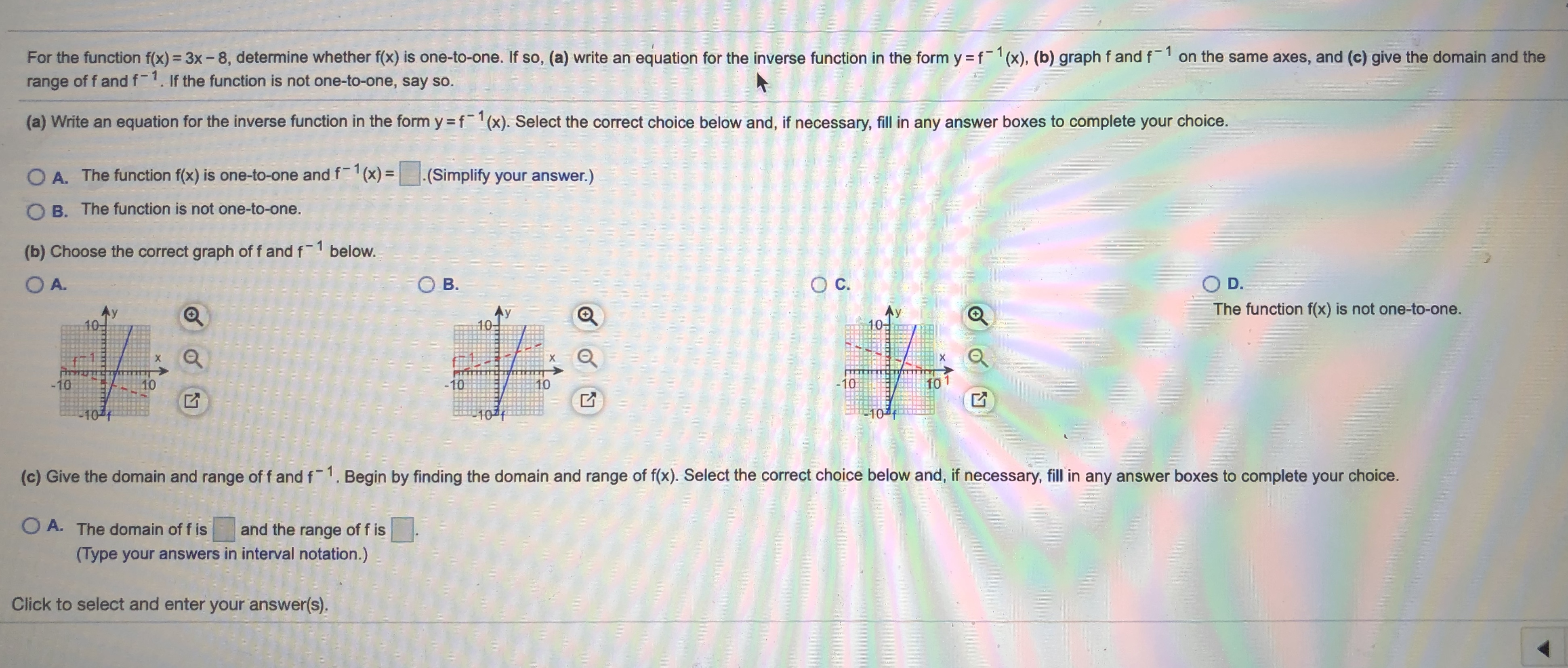



Answered For The Function F X 3x 8 Bartleby




Example 15 F X 1 X What Is The Domain And Range Examples




What Are The Domain And Range Of F X 1 5 X Brainly Com
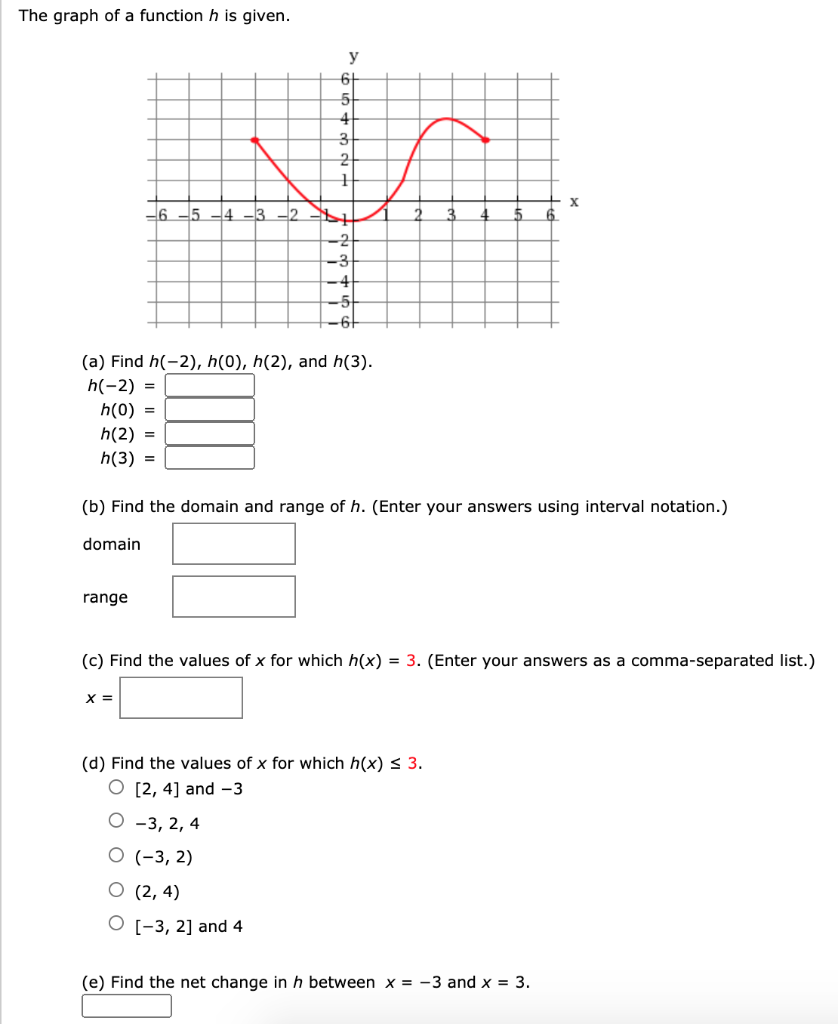



What Is The Range Of X 3




Find The Range Of Each Of The Following Functions F X X 3 F X 1 X 2 F X X 4 Youtube




Example 15 F X 1 X What Is The Domain And Range Examples
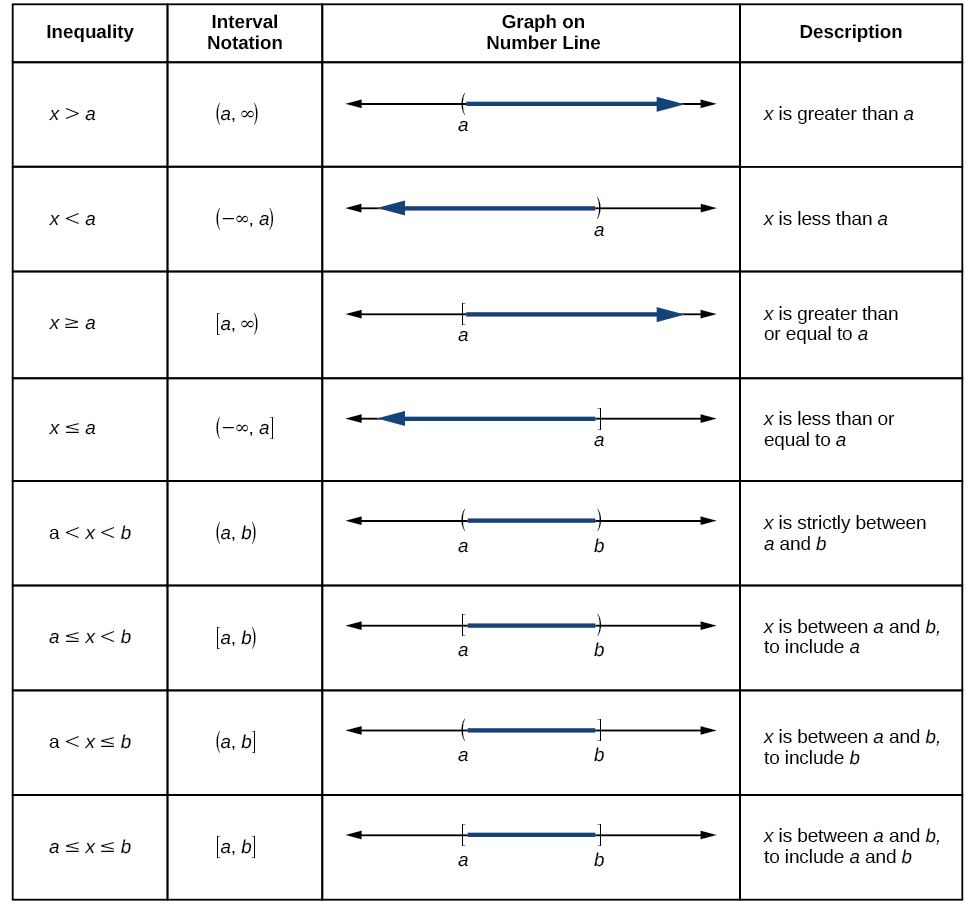



Domain And Range Algebra And Trigonometry




6 Ways To Find The Domain Of A Function Wikihow




Downloaded From Equations 2 4 The Reciprocal Function X 1 X Pdf Free Download




Find The Range Of I F X X 4 X 4 And Domain Of Ii F X




Domain And Range Of 1 X 2 2x 8 Youtube




Misc 4 Find Domain And Range Of F X Root X 1 Chapter 2




Domain And Range Of Quadratic Functions Video Khan Academy




Find The Domain And Range Of The Real Function Defined By F




Find The Domain Or Range Of Following Function Tex F X Sqrt X 1 3 X Tex Brainly In



How Do You Find The Domain And Range Of Y Sqrt 3x 5 Socratic
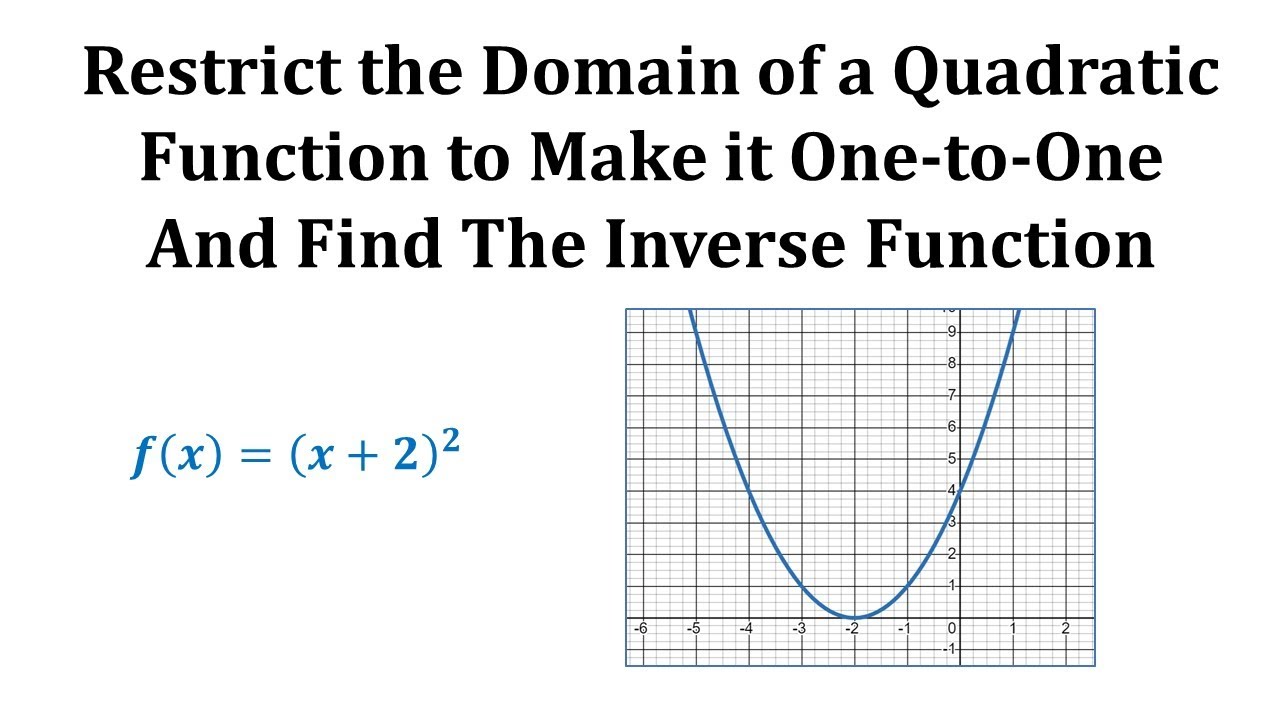



Ex Restrict The Domain To Make A Function 1 To 1 Then Find The Inverse Youtube




Find The Domain And Range Of F X Sin 1 X X Where
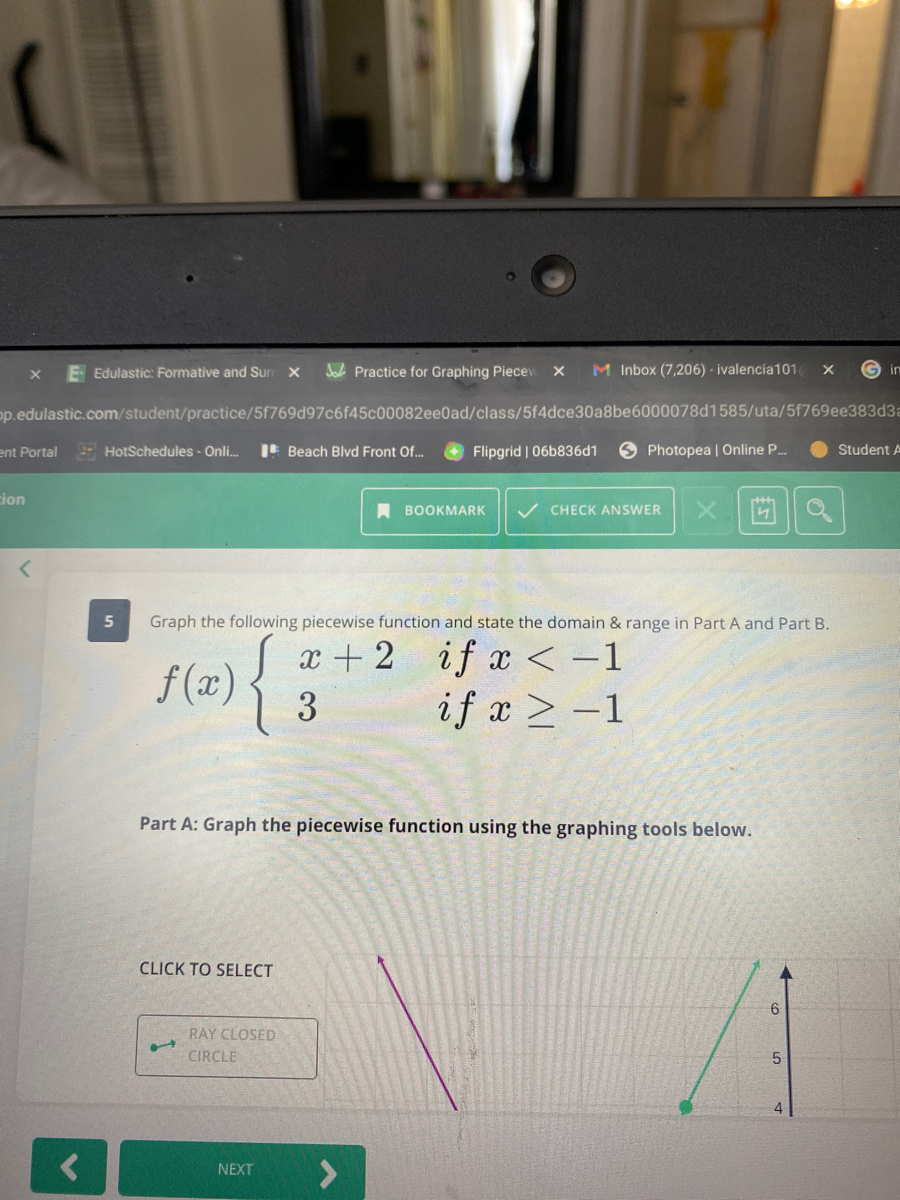



Answered Graph The Following Piecewise Function Bartleby



What Is The Range Of A Function Expii




Answered 3x For 1 X 1 Let F X X 4 For Bartleby




Domain And Range Of F X X 3 X 3 Are Respectively




Domain Range Of Functions Graphs Calculator Examples Cuemath




Find Domain And Range Of Real Functions 1 F X X 2 3 X 2




How To Find The Domain Of A Function Video Khan Academy




Ex 2 2 6 Determine Domain And Range Of R X X 5



Domain Range A Function
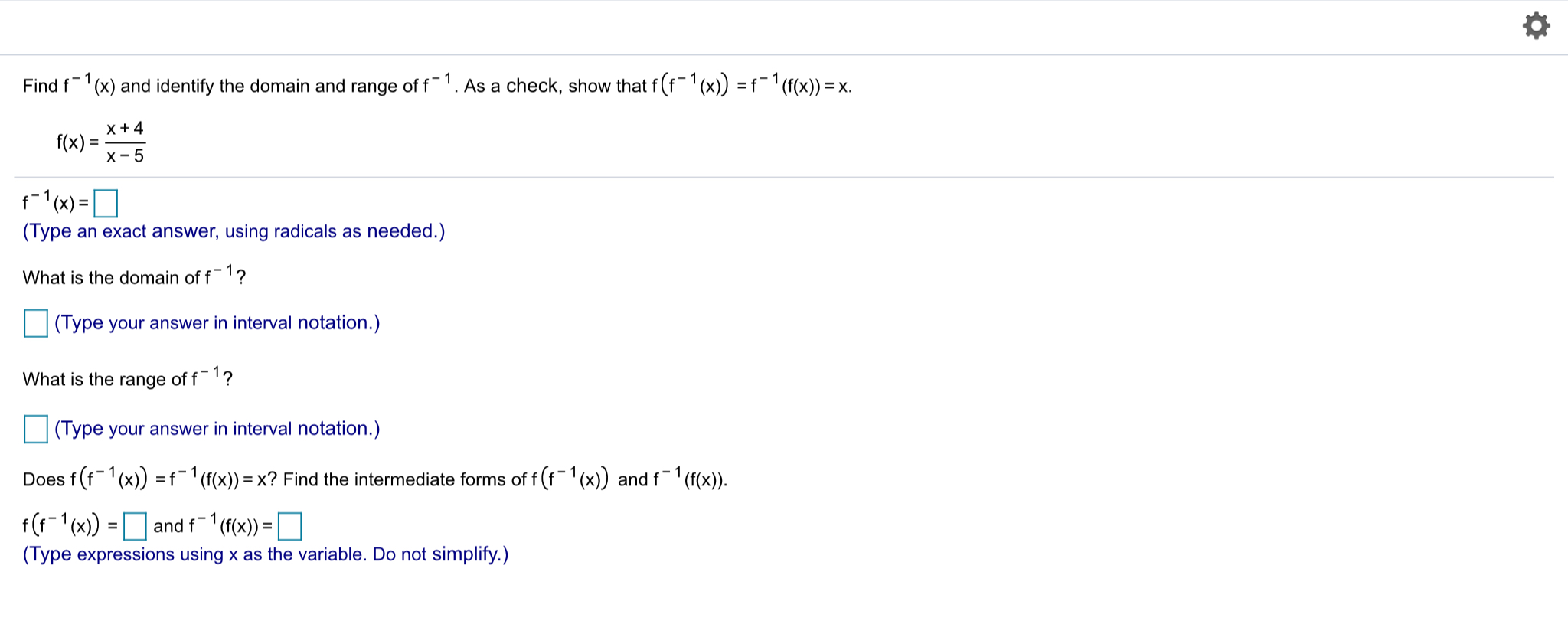



Solved Find F 1 X And Identify The Domain And Range Of F Chegg Com




Find The Domain And Range Of The Inverse Of The Given Chegg Com




Find The Domain And Range Of The Function F X 1 1 X 2 X I




F X 2x 1 Find Domain And Range Brainly In




Find Domain And Range Of F X 1 16 X 2 Brainly In




Find The Domain Of The Function F X 2cos 1 2x Sin 1 X




Domain Range A Find The Natural Domain 3 1 F X Chegg Com




Igcsefm Domain Range Ppt Download



What Is The Domain And Range Of F X X 1 X 2 1 X 3 Quora




Oneclass Determine The Inverse Of F X 2x 1 X 5 Include The Domain And Range For F 1 X



What Is The Range Of F X X 1 X 1 Quora




Chapter 1 Functions Asymptote Function Mathematics




Find The Domain And Range Of The Function F X 1 5 X Brainly In




Find Domain And Range Of Real Functions 1 F X X 2 3 X 2 F X 1 Sqrt X 5 Youtube




Igcsefm Domain Range Ppt Download




Find The Domain And Range Of F X Square Root Of X 2 3x 2 Maths Relations And Functions Meritnation Com




Find The Domain And Range Of 𝑓 𝑥 1 4𝑥 2 1 Maths Relations And Functions Meritnation Com
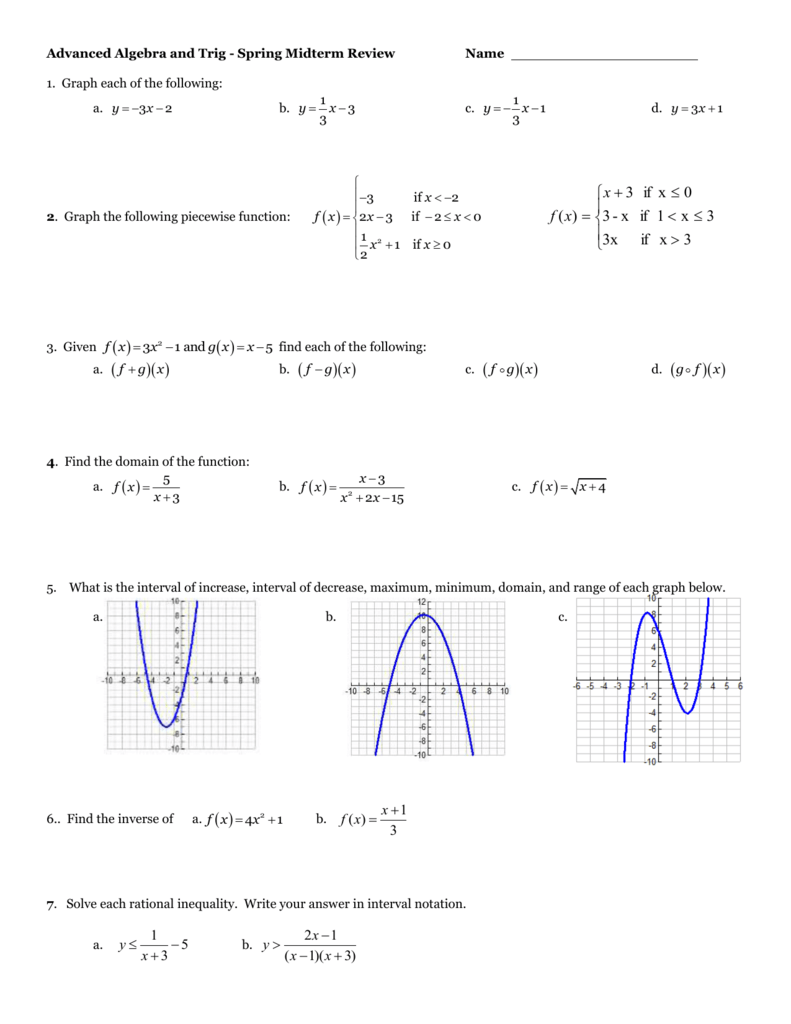



Advanced Algebra And Trig




Misc 3 Find Domain Of F X X2 2x 1 X2 8x 12



0 件のコメント:
コメントを投稿